微分

---

确定一个函数的导数的过程；又叫求导数。

导数的概念与边际的概念很接近。边际概念可定义为与自变量的一个单位相关的因变量的变化。通过一个函数y=f(x)中变化的特性更精确地说明这一关系，用△x表示自变量x值的变化，用△y表示因变量y值的变化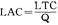，的比值最概括地反映了上述边际概念。

求导数就是在自变量极小的场合下求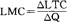的比值。

导数的数学符号是：

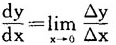
其读法是"当△x接近零时，y对x的导数等于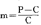比值的极限。"

导数作为比值极限的概念恰好等于曲线上某一点的斜率。

附图示出这个概念。

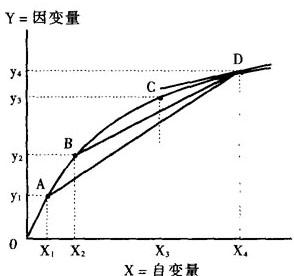
导数作为曲线斜率的示意图

图中的曲线在A点与D点之间的平均斜率测定如下：

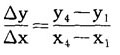
这个平均斜率表现为连接两点的弦的斜率。同样，它可在x值的更小的区间加以测定，并用其他弦来表示。

在到达极限时，即当△x接近零时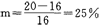，比值等于在曲线的D点上所作切线的斜率。

这条切线的斜率定义为函数在D点的导数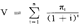，它测定与x值的一个很小的变化相联系的y值的边际变化。

微分是一种很好的分析方法，它通过边际分析可用来确定目标函数的最大值与最小值，提供管理经济学方面的有用信息，特别易于推广应用于解决管理决策中约束最佳化的问题。

确定一个函数的导数只要对函数应用一个基本公式就行，它在微积分教程中可以找到。