7.2.1 四则运算的微分
若c为常数,函数u(x),v(x)都有导数,则
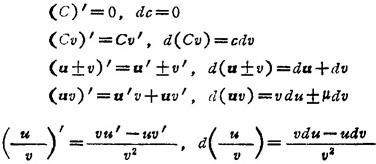
7.2.2 复合函数的导数
若y=f(u),u=φ(x)都有导数,则
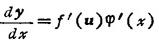
7.2.3 反函数的导数
若函数y=f(x)在点x处有不为零的导数,且反函数x=f-1(y)在此点连续,则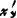 存在且
存在且
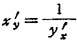
7.2.4 隐函数微分法则
设函数F(x,y)连续,且对每个自变量都有连续的偏导数,而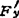 (x,y)
(x,y)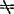 0
0
则由F(x、y)=0所决定的函数y=y(x)的导数
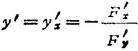
式中
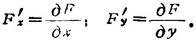
7.2.5 用参数表示的函数的微分法则
设φ(t)、ψ(t)为可微函数,且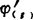 ≠0,则由参数方程
≠0,则由参数方程
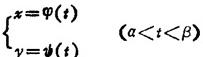
所决定的x的单值连续函数y=Ψ〔φ-1(x)〕的导数:
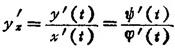
- 弗雷姆是什么意思
- 弗雷姆是什么意思
- 弗雷尔是什么意思
- 弗雷尼奥是什么意思
- 弗雷德是什么意思
- 弗雷德里克·巴师夏是什么意思
- 弗雷恩是什么意思
- 弗雷恩是什么意思
- 弗雷斯是什么意思
- 弗雷斯塔德是什么意思
- 弗雷曼是什么意思
- 弗雷格是什么意思
- 弗雷格是什么意思
- 弗雷格是什么意思
- 弗雷格是什么意思
- 弗雷格是什么意思
- 弗雷格是什么意思
- 弗雷格,戈特洛布是什么意思
- 弗雷格.戈特洛布是什么意思
- 弗雷歇特是什么意思
- 弗雷歇特是什么意思
- 弗雷泽是什么意思
- 弗雷泽是什么意思
- 弗雷泽是什么意思
- 弗雷泽是什么意思
- 弗雷泽是什么意思
- 弗雷泽是什么意思
- 弗雷泽是什么意思
- 弗雷泽是什么意思
- 弗雷泽是什么意思
- 弗雷泽·詹是什么意思
- 弗雷泽,乔是什么意思
- 弗雷泽,彼是什么意思
- 弗雷泽,彼得是什么意思
- 弗雷泽,西是什么意思
- 弗雷泽,詹姆斯·乔治,爵士是什么意思
- 弗雷舍尔是什么意思
- 弗雷西内计划是什么意思
- 弗雷诺是什么意思
- 弗雷里是什么意思
- 弗雷隆是什么意思
- 弗雷雷是什么意思
- 弗鲁克托索·里维拉是什么意思
- 弗鲁博顿是什么意思
- 弗鲁戈尼·盖罗洛是什么意思
- 弗鲁瓦萨尔是什么意思
- 弗鲁科夫斯基是什么意思
- 弗鲁贝尔是什么意思
- 弗鲁赞法尔是什么意思
- 弘是什么意思
- 弘是什么意思
- 弘一是什么意思
- 弘一大师是什么意思
- 弘一大师书信手稿选集是什么意思
- 弘一大师书华严集联是什么意思
- 弘一大师全集是什么意思
- 弘一大师李叔同书信集是什么意思
- 弘一大师遗墨是什么意思
- 弘一法师是什么意思
- 弘一法师是什么意思