快速傅立叶变换

---

11．3．1 有限离散傅立叶变换的不同形式

见表1．1－17。

表1．1－17 有限离散傅立叶变换的不同形式

11．3．2 快速傅立叶变换算法

快速傅立叶变换算法(简称FFT算法)，是计算有限离散傅立叶变换的快速方法。

❶  复序列的FFT算法。计算复序列｛zk｝(k=0，1，…，N－1)的有限离散傅立叶变换(hd=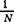)，就是计算形如

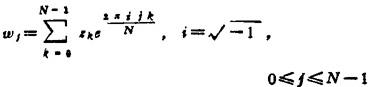
的有限项和。对于反演公式，计算方法类似。

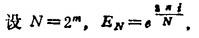
则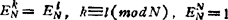

又设 k=(k_m－1…k₁k₀)=k_m－12^m－1+…+k₁·2+k₀

j=(j_m－1…j₁j₀)=j_m－12^m－1+…+j₁．2+j₀

分别是k和j的二进制表示，k_p，j_p取值为0或1，ρ=0，1，2，…，m－1。

复序列｛z_k｝计算的递推公式为

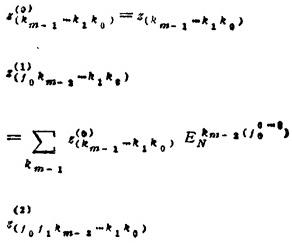
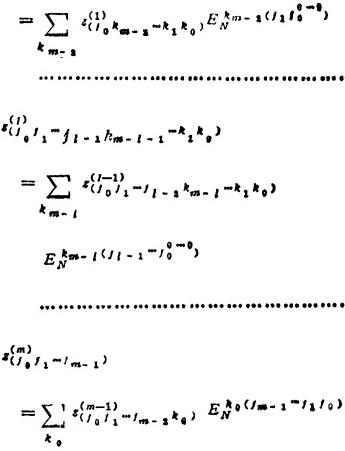
并且有

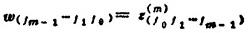
❷ 实序列的FFT算法。设有2N(N=2m)个元素构成的实序列｛ηk｝(k=0，1，2，…2N－1)，要计算｛ηk｝的有限离散傅立叶余弦变换和正弦变换

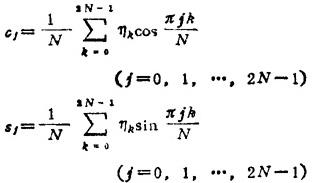
可先用EFT算法关于复序列z_k=x_k+iyk(x_k=η_2k，y_k=η_2k+1)计算

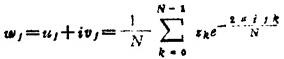
而c_j，s_j用下列公式计算

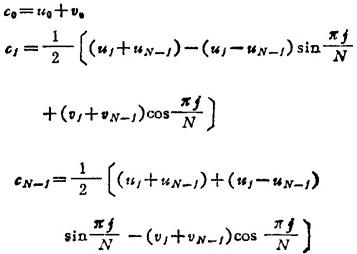
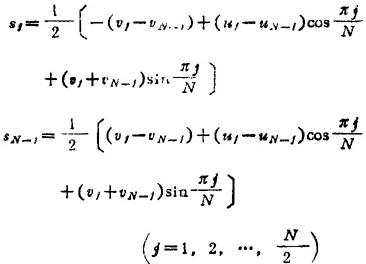
c_j，s_j当j=N，N+1，…，2N－1时的数值分别为

cN=uN－vN，sN=0

c_2N－j=c_j，s_2N－f=－s_j(j=1，2，…，N－1)