快速富氏变换

---

给定实的或复的序列f₀，f₁，…f_n－1，则

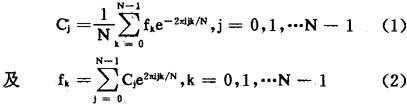
其中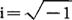，为一对互逆的变换，若把由｛f_k｝求｛C_i｝的过程(1)称为有限离散富氏变换，则由｛C_j｝求｛f_k｝的过程(2)就被称为逆富氏变换。

例如，设f(X)是以2π为周期的复函数，已知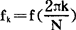，k=0，1，…N－1，则满足插值条件：

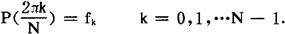
的三角多项式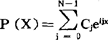，其系数｛Cj｝与｛f_k｝就构成了一对互逆的有限富氏变换(1)与(2)。

对于(2)的计算，令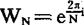，若不计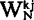的计算量，直接计算

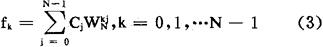
需用N²个复数乘法，当N较大时这是个不小的数目，为了减少乘法的运算次数，下面介绍一种常用的快速算法，它只须(1og₂N－1)N／2次乘法，从而大大加快了运算速度。

取N=2^p(p是正整数)，记C(j)=C_j，整个算法由p个递推关系给出：

对于(1)的计算，只要令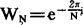，可按上述步骤同样的进行。