研究数论函数的性质及数论函数之间关系的重要方法。
在筛法等问题中有许多重要应用。最重要的数论变换是狄里克利乘积。
设f(n)与g(n)是两个数论函数,则称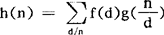 为f(n)与g(n)的狄里克利乘积或卷积,记作h=f*g。
为f(n)与g(n)的狄里克利乘积或卷积,记作h=f*g。
例如,设u(n)≡1,n≥1;1(1)=1,n>1时,I(n)=0;μ(n)为茂陛乌斯函数,即当n=1时,μ(n)=1,当n=p1p2…ps,(p1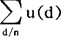 当n=1时为1,当n>1时为0,所以单位函数I(n)是茂陛乌斯函数与u(n)的狄里克利乘积、狄里克利乘积的一个重要性质是它满足结合律和交换律,亦即,若f,g,h为任意三个数论函数,则f*g==g*f,(f*g)*h=f*(g*h),狄里克利乘积作为数论函数之间的一种重要运算,其逆运算同样也是十分重要的,其中最重要的就是所谓狄里克利逆。
当n=1时为1,当n>1时为0,所以单位函数I(n)是茂陛乌斯函数与u(n)的狄里克利乘积、狄里克利乘积的一个重要性质是它满足结合律和交换律,亦即,若f,g,h为任意三个数论函数,则f*g==g*f,(f*g)*h=f*(g*h),狄里克利乘积作为数论函数之间的一种重要运算,其逆运算同样也是十分重要的,其中最重要的就是所谓狄里克利逆。
设f(n)为数论函数,若存在一个数论函数g(n),使得f*g=I,则称g(n)为f(n)的狄里克利逆,并记g(n)=f1-1(n),例如,由于μ*u=1,所以μ(n)的逆为u(n)≡1,u(n)的逆则为μ(n)。
狄里克利乘积中,应用最广泛的是它的特例,即茂陛乌斯变换,若F=f*u,即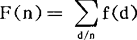 ,则称F为f的茂陛乌斯变换,例如,I(n)就是μ(n)的茂陛乌斯变换;除数函数
,则称F为f的茂陛乌斯变换,例如,I(n)就是μ(n)的茂陛乌斯变换;除数函数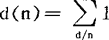 则是u(n)的茂陛乌斯变换;恒等函数e(n)=n,n≥1就是欧拉函数φ(n)的茂陛乌斯变换,亦即
则是u(n)的茂陛乌斯变换;恒等函数e(n)=n,n≥1就是欧拉函数φ(n)的茂陛乌斯变换,亦即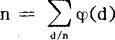 ;若
;若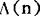 为蒙哥尔特函数,即当n=pk,k≥1时,
为蒙哥尔特函数,即当n=pk,k≥1时,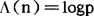 ,对其它的n,
,对其它的n,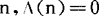 ,则logn为
,则logn为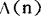 的茂陛乌斯变换,亦即
的茂陛乌斯变换,亦即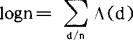 ,茂陛乌斯变换的一个重要性质是:若F=f*u,则f=F*μ,亦即若
,茂陛乌斯变换的一个重要性质是:若F=f*u,则f=F*μ,亦即若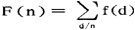 ,则有
,则有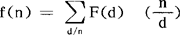 ,由此便可得到
,由此便可得到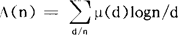 及
及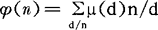 等重要公式,茂陛乌斯变换的另一个重要性质是:f(n)的茂陛乌斯变换F(n)为可乘函数的充分必要条件是f(n)为可乘函数,因此,当f(n)为可乘时,就有
等重要公式,茂陛乌斯变换的另一个重要性质是:f(n)的茂陛乌斯变换F(n)为可乘函数的充分必要条件是f(n)为可乘函数,因此,当f(n)为可乘时,就有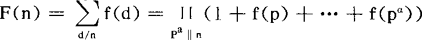 ,由此便立即可以得到
,由此便立即可以得到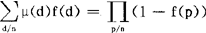 ,
,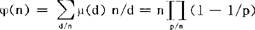 以及
以及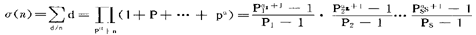 等重要公式。
等重要公式。
- 绸子做的袄是什么意思
- 绸子盖地是什么意思
- 绸完索南扎西是什么意思
- 绸密是什么意思
- 绸布店是什么意思
- 绸布征是什么意思
- 绸帛的衣是什么意思
- 绸带是什么意思
- 绸带兵刃是什么意思
- 绸床罩是什么意思
- 绸披披是什么意思
- 绸料是什么意思
- 绸沓是什么意思
- 绸直是什么意思
- 绸纹相纸是什么意思
- 绸纽扣是什么意思
- 绸绢画是什么意思
- 绸绸是什么意思
- 绸绸子是什么意思
- 绸缎是什么意思
- 绸缎庄是什么意思
- 绸缪是什么意思
- 绸缪。是什么意思
- 绸缪(唐风)是什么意思
- 绸缪帐扆是什么意思
- 绸缪帷帐是什么意思
- 绸缪帷幄是什么意思
- 绸缪未雨是什么意思
- 绸缪束薪是什么意思
- 绸缪束薪,三星在天(今夕何夕,见此良人。)是什么意思
- 绸缪桑土是什么意思
- 绸缪牖户是什么意思
- 绸缪缱绻是什么意思
- 绸舞是什么意思
- 绸衫是什么意思
- 绸袄是什么意思
- 绸面被是什么意思
- 绸顺是什么意思
- 绹是什么意思
- 绹倒是什么意思
- 绹索纹罍是什么意思
- 绹索纹铜罍是什么意思
- 绹绞是什么意思
- 绹绳是什么意思
- 绹铃是什么意思
- 绹鸟子是什么意思
- 绺是什么意思
- 绺儿是什么意思
- 绺儿匠/娃子是什么意思
- 绺娃是什么意思
- 绺娃子是什么意思
- 绺子是什么意思
- 绺子手是什么意思
- 绺子风是什么意思
- 绺手是什么意思
- 绺窃是什么意思
- 绺绺是什么意思
- 绺绺/子是什么意思
- 绺绺子是什么意思
- 绺行是什么意思