亦称“线积分”。
禷指拍畹耐乒恪I?I>f(x,y)是定义于曲线l上的函数,将l任意划分为n段小弧l1,l2,…,ln,记lk的弧长为Δsk,在l上任取一点(xk,yk),作和式
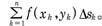
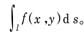
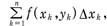
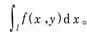
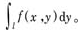 以上的概念还可以推广到高维空间。曲线积分通常可以化为定积分进行计算。
以上的概念还可以推广到高维空间。曲线积分通常可以化为定积分进行计算。- 凯勒是什么意思
- 凯塞林是什么意思
- 凯奇是什么意思
- 凯恩是什么意思
- 凯恩斯是什么意思
- 凯捷是什么意思
- 凯撒是什么意思
- 凯撒大帝是什么意思
- 凯旋是什么意思
- 凯旋而归是什么意思
- 凯旋门是什么意思
- 凯歌是什么意思
- 凯泽是什么意思
- 凯特尔是什么意思
- 凯特林是什么意思
- 凯瑟是什么意思
- 凯莱是什么意思
- 凯诺是什么意思
- 凯鲁亚克是什么意思
- 凰是什么意思
- 凳是什么意思
- 凳子是什么意思
- 凶是什么意思
- 凶事是什么意思
- 凶人是什么意思
- 凶信是什么意思
- 凶兆是什么意思
- 凶光是什么意思
- 凶器是什么意思
- 凶多吉少是什么意思
- 凶嫌是什么意思
- 凶宅是什么意思
- 凶巴巴是什么意思
- 凶年是什么意思
- 凶徒是什么意思
- 凶恶是什么意思
- 凶悍是什么意思
- 凶戾是什么意思
- 凶手是什么意思
- 凶暴是什么意思
- 凶杀是什么意思
- 凶杀案是什么意思
- 凶案是什么意思
- 凶横是什么意思
- 凶死是什么意思
- 凶残是什么意思
- 凶毒是什么意思
- 北京航空航天大学是什么意思
- 北京话是什么意思
- 北京车站是什么意思
- 北京邮电大学是什么意思
- 北京鸭是什么意思
- 北仑港是什么意思
- 北伐是什么意思
- 北伐军是什么意思
- 北伐战争是什么意思
- 北侧是什么意思
- 北关是什么意思
- 北冰洋是什么意思
- 北半球是什么意思