指两个互斥事件之和的概率等于各个事件概率之和。
设已知事件A出现的概率为p(A),事件B出现的概率为p(B),则在n次试验中,事件A出现的次数应为np(A),事件B出现的次数应为np(B)。又因事件A与B不能同时出现,故在n次试验中,A或B任意一个出现的次数为:np(A)+np(B),因而
gp(A+B)=p(A)+p(B)
这个结论推广到互斥的有限个事件,则两两互斥的有限个事件之和的概率等于这些事件的概率之和。用公式表示为:
p(A1+A2+……+An)=p(A1)+p(A2)+……+p(An)
A和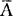 构成完备事件组,所以
构成完备事件组,所以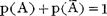 。
。
即任一随机事件A的概率恒等于1减去其对立事件Ä的概率。
亦即: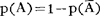
- 瑶族耍歌堂是什么意思
- 瑶族自称是什么意思
- 瑶族舞曲是什么意思
- 瑶族语言简志是什么意思
- 瑶族达努节是什么意思
- 瑶族过山榜选编是什么意思
- 瑶族风情录是什么意思
- 瑶林一枝是什么意思
- 瑶林琼圃是什么意思
- 瑶林琼树是什么意思
- 瑶民起义是什么意思
- 瑶池是什么意思
- 瑶池玉液是什么意思
- 瑶池璇宫是什么意思
- 瑶池都督府是什么意思
- 瑶池阆苑是什么意思
- 瑶浆蜜勺,实羽些。是什么意思
- 瑶溪是什么意思
- 瑶溪镇是什么意思
- 瑶环瑜珥是什么意思
- 瑶琳仙境是什么意思
- 瑶琳仙境是什么意思
- 瑶瑟夫人是什么意思
- 瑶瑟怨是什么意思
- 瑶石山人稿是什么意思
- 瑶老制是什么意思
- 瑶花是什么意思
- 瑶芳(金枝公主)是什么意思
- 瑶草是什么意思
- 瑶草琪花是什么意思
- 瑶觞是什么意思
- 瑶觞记是什么意思
- 瑶语是什么意思
- 瑶语支是什么意思
- 瑶语支是什么意思
- 瑶里孛迭是什么意思
- 瑶里孛迭是什么意思
- 瑶里谈判是什么意思
- 瑶钟是什么意思
- 瑶锦是什么意思
- 瑷珲是什么意思
- 瑷珲保卫战是什么意思
- 瑷珲保卫战是什么意思
- 瑷珲条约是什么意思
- 瑸都是什么意思
- 璂是什么意思
- 璃是什么意思
- 璆是什么意思
- 璇子是什么意思
- 璇室是什么意思
- 璇玑是什么意思
- 璇玑图是什么意思
- 璇玑图诗是什么意思
- 璇霄流沆瀣之精是什么意思
- 璇题是什么意思
- 璇题藻井穷丹青,玉笙宝瑟声冥冥。是什么意思
- 璋是什么意思
- 璋是什么意思
- 璋是什么意思
- 璋珪杂于甑窐兮,陇廉与孟娵同宫。是什么意思