正项级数判敛法

---

收敛准则：正项级数部分和S_n有界者必收敛。

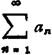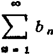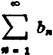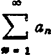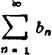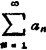比较法：两个级数及中，若a_n≤b_n，且收敛，则也收敛；若a_n≥b_n，而 且发散，则也发散。

比值法如下：

❶ 达朗贝尔判别法，设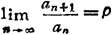，则当p＜1时极数收敛；当p＞1时级数发散；当p=1时不能肯定，

❷ 拉阿伯判别法。设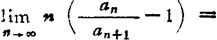φ，则当p＞1时，级数收敛；当ρ<1时，级数发散，当ρ=1时不能肯定。

❸ 高斯判别法，设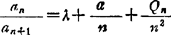，其中，λ，α为常数：Q_n为有界量，则当λ≥1且α>1时，级数收敛；当λ≤1且α≤1时，级数发散．

柯西判别法如下：

❶ 根值判别法。设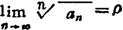，则当ρ＜1时级数收敛；当ρ＞1时，级数发散；当ρ=1时，不定。

❷ 积分判别法．若a_n=f(n)，且f(x)在〔1．∞)上是正的单调递减的连续函数，则当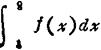存在时，级数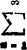收敛；当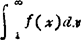不存在时，级数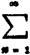发散。