牛顿法

---

给定非线性方程组

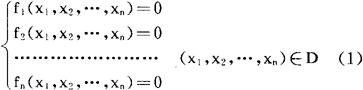
记Z=〔x₁，x₂，…，x_n〕^T，F(x)=〔f₁(x)，f₂(x)，…f_n(x)〕^T，则组(1)可简记为

F(X)=0 X∈D (2)

在一定的条件下，牛顿法可较快的求得(1)的解X^*。

设X^(K)是X^*的第K次近似，假设f_i(x₁，x₂，…，X_n)，i=1，2，…，n，在X^*∈D的某个凸域中连续且有连续的一阶偏导数，则有

F(X)=F(X^(k)+F’(X^(K))(X－X^(k))+0(‖XX^(K)‖)，

其中

。

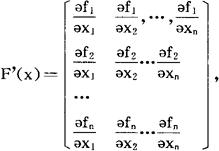
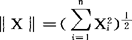略去高阶无穷小量，得到(2)的近似方程：

F(X^(k))+F′(X^(k)(X－X^(k))=0 (3)

这是个线性方程组。

若F’(X^(k))≠0，它的解就是X^*的第K+1次近似，即

X^(K+1)=X^(K)－F’(X^(k))^－1F(X^(K)) (4)

K=0，1，2，…

(4)就是解方程组(1)的牛顿迭代程序，其中X⁽⁰⁾为初值，一般要求X⁽⁰⁾充分接近X^*。迭代过程当满足‖F(X^(k)‖＜ε₁，及‖X^(k+1)－X^(K)‖＜ε₂‖X^(k)‖时，就可停止。(ε₁，ε₂是给定的精度要求)。

牛顿迭代程序的特点是收敛速度快，若F’(X)在点X*处满足Lipschitz条件，即存在正常数K使‖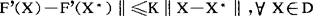则牛顿序列｛XK｝至少平方收敛于X^*。