磁铁周围存在磁场早为人们所发现,历史上很长一段时间里,磁与电被认为是两类截然分开的现象,直到19世纪初,人们才认识到电与磁之间有著不可分割的联系。
所有的磁场都是由电流或运动电荷产生的(根据安培分子环流假说,磁铁与磁场,物质的磁性,都是分子环流导致的)。运动著的电荷之间不单存在库仑相互作用,还同时存在著磁相互作用。在磁学中,与库仑定律相当的是安培定律,即距电流元I1dl1为r12的电流元I2dl2所受到前者的磁作用力为
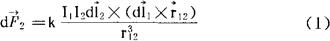
式中k是取决于单位制的普适常数。
上式也可写成
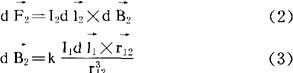
(3)式所示的dB2称为电流元I1dI1在I2dl2所在处r2所产生的磁感应强度。
考虑到空间存在多种电流,则这些电流在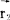 所产生的总磁感应强度应为(毕奥萨伐尔定律)
所产生的总磁感应强度应为(毕奥萨伐尔定律)
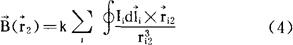
此时(2)推广为
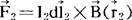 (5)
(5)
(5)式表明,与电学中用检验电荷来检测电场类似,磁学中原则上可以用电流元Idl来检验磁场,在实验中当然不可能有孤立的电流元,但可用采用小面积的平面载流圈来检验磁场,可以证明,面积为S、共N匝、所通电流为Ⅰ的线圈在磁场受到一个力矩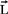 的作用,
的作用,
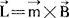
式中\\是与线圈电流成右手系的法向)称为该载流线圈的磁矩。
与电场类似,根据磁场的特点,可引起所谓矢势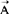 ,它与
,它与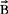 的关系为
的关系为
 (6)
(6)
然后建立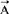 的微分方程(其形式与泊松方程相似,只是这里的源应改为电流密度,另外还带一个与单位制有关的常系数),结合边界条件解该方程并从
的微分方程(其形式与泊松方程相似,只是这里的源应改为电流密度,另外还带一个与单位制有关的常系数),结合边界条件解该方程并从
(6)式求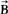 ,这样计算有时比直接从(4)式计算更为方便有效。
,这样计算有时比直接从(4)式计算更为方便有效。
- 散郎是什么意思
- 散风丹是什么意思
- 散风止痒汤是什么意思
- 散风活络丸是什么意思
- 散风清热丸是什么意思
- 散风燥湿解毒汤是什么意思
- 散风除湿丸是什么意思
- 散马休牛是什么意思
- 散骑常侍是什么意思
- 散骑常侍是什么意思
- 敦是什么意思
- 敦是什么意思
- 敦是什么意思
- 敦是什么意思
- 敦仁堂医案 清 沈潞是什么意思
- 敦促杜聿明等投降书是什么意思
- 敦刻尔克大撤退是什么意思
- 敦刻尔克撤退是什么意思
- 敦化乌头是什么意思
- 敦化乌头是什么意思
- 敦厚的诈骗犯是什么意思
- 敦复汤是什么意思
- 敦复汤是什么意思
- 敦夙好斋诗初编是什么意思
- 敦巴顿橡树园会议是什么意思
- 敦庞是什么意思
- 敦庞是什么意思
- 敦弓是什么意思
- 敦忍乙是什么意思
- 敦拜是什么意思
- 敦本堂是什么意思
- 敦煌是什么意思
- 敦煌是什么意思
- 敦煌是什么意思
- 敦煌是什么意思
- 敦煌不畏刀兵写经残卷是什么意思
- 敦煌丛刊初集是什么意思
- 敦煌中医药全书是什么意思
- 敦煌于阗文遗书与仲云是什么意思
- 敦煌于阗文遗书与仲云是什么意思
- 敦煌五台山文献校录研究是什么意思
- 敦煌佛爷庙一新店台晋墓群是什么意思
- 敦煌佛说大药善巧方便经卷上是什么意思
- 敦煌俗讲文学及通俗小说总目提要是什么意思
- 敦煌六朝写本春秋经传集解是什么意思
- 敦煌写本古文孝经残卷是什么意思
- 敦煌写本守温韵学残卷是什么意思
- 敦煌写本校春秋正义衔名是什么意思
- 敦煌写本真草千字文是什么意思
- 敦煌写本篆书千字文是什么意思
- 敦煌写本论语卷首是什么意思
- 敦煌出土十诵比丘尼波罗提木叉戎本是什么意思
- 敦煌出土文学文献分类目录附解说是什么意思
- 敦煌劫余录是什么意思
- 敦煌医粹是什么意思
- 敦煌千佛洞回鹘文文献是什么意思
- 敦煌千佛洞的中兴是什么意思
- 敦煌县志 (道光)是什么意思
- 敦煌变文是什么意思
- 敦煌变文是什么意思