符号检验

---

非参数检验的一种。

用于检验两个相关变量Y₁与Y₂(均为等距变量)在数值上“差异是否为零”。它利用差数的符号个数构造统计量，故称。对n个样品观测Y₁与Y₂，得到样本资料：(Y₁₁，Y₂₁)，(Y₁₂，Y₂₂)，…，(Y_1n，Y_2n)。考虑差数的符号Sign(Y₁-Y₂)=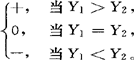要检验的假设是H₀：P_r(Y₁＞Y₂)=P_r(Y₁＜Y₂)；H₁：P_r(Y₁＞Y₂)≠P_r(Y₁＜Y₂)。

若Y₁与Y₂在数值大小上无显著差异，则样本中正号的差数个数与负号的差数个数应当很接近。记n+是样本中正号差数个数，n－是负号差数个数(注意：n++n－≤n)。我们再记r=min｛n+，n－｝，则当r不太小时，有利于H₀，当r太小，则有利于H₁。可查《符号检验的r临界值表》，查出临界值r_a。

若r＞r_a，则接受H₀，否则，拒绝H₀。

一般样本容量n≤25时，可查表进行符号检验。该表实际是由二项分布计算得来，但当n＞25时，二项分布接近正态分布，故可用下面方法作检验。记T为正号差数个数。

由统计理论得知，T的极限分布是平均数为n／2，方差是n／4的正态分布，于是选用的检验统计量为Z=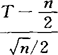=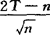，在H₀成立时它趋近于标准正态分布，但为使Z更具连续性(因为T是离散变量)，常采用修正的Z：Z=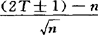，当T＜n／2时，上式中括号内取正号；当T＞n／2时，则取负号。