纳维—斯托克斯方程

---

纳维—斯托克斯方程就是粘性不可压缩流体动量守恒的运动方程，简称N－S方程。该方程概括了粘性不可压缩流体流动的普遍规律，因此具有特别重要的意义。

(1)矢量式

式中 ▽²——拉普拉斯算子，在直角坐标系中为

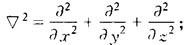
v——流体的运动粘度；

F_m——质量力；

p——流体各向同性压力；

v——流体速度矢量。

(2)直角坐标系标量式

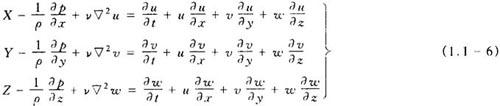
式中 X，Y，Z——单位质量的质量力在x，y，z方向的分量；

u，v，w——速度矢量v在x，y，z方向的分速度。

(3)圆柱坐标系标量式

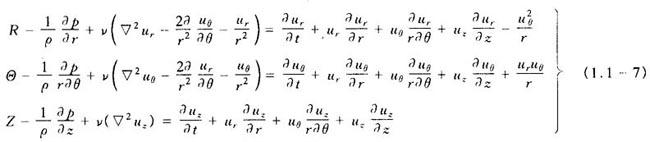
式中 R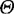，，Z——单位质量的质量力在r，θ，z方向的分量；

▽²——拉普拉斯算子，在圆柱坐标系中为

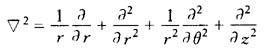
以上三组方程，若不计粘性的作用，即设v=0，则可得到相应的理想流体的运动微分方程式，即欧拉运动微分方程。