线性规划模型标准化

---

线性规划标准化模型即可直接用单纯形进行运算的模型形式。

对于非标准形式的线性规划模型，不能直接由单纯形法求解，必须通过处理转换成标准形式。常见到的有下面几种情况：

(1)目标函数Min化问题

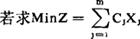
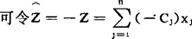
则求MinZ相当于求解MAXZ

(2)不同类型约束条件处理方式

❶ “≤”约束条件

通过引入松弛变量，可将“≤”约束变为要求的等式形式

如：5x₁+8x₂≤100可引入非负的松弛变量x₃，转化成：

5x₁+8x₂+x₃=100

❷ “=”约束条件

通过引入人工变量，可将约束转变为要求的等式形式

如：5x₁+8x₂=100，可引入非负的人工变量x₃，转化成：

5x₁+8x₂+x₃=100

❸ “≥”约束条件

通过引入剩余变量，首先将其转化成等式。

再作等式处理，引入人工变量，变成所需形式。

如：5x₁+8x₂≥100，可引入非负的剩余变量x₃和人工变量x₄，转化成：

5x₁+8x₂－x₃+x₄=100

(3)模型中有自由变量

自由变量即可能大于0，也可能小于0，亦可能等于0的变量，这种变量不满足求解模型对变量非负的要求。可作如下处理：

若x_j为自由变量

可设X′_j，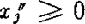

且令x_j=x′_j－x_j″

将原模型中x_j处用X′_j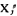－代换，对新的模型求解，再由解得的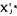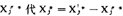，得到自由变量X_j的解。

〔参〕线性规划单纯形法