统计估计

---

利用样本资料对总体参数进行估计，或在有一定相关关系的随机变量之间，按一定的准则，根据一些随机变量对另一随机变量作最佳估计与预测。

设总体x的分布函数为F(x；θ)，其中x₁为x的观测值，θ为未知参数，θ的取值范围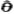为参数空间。由子样x₁，x₂，…，x_n建立不带有未知参数的统计量f(x₁，x₂，…，x_n)对未知参数θ做出最佳估计，即为参数估计。

参数估计分为点估计和区间估计两类。

称f(x₁，x₂，…，x_n)为θ的估计量，记作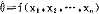。对于子样观测值(x₁，x₂，…，x_n)，称t=f(x₁，x₂，…，x_n)为θ的估计值，建立统计量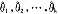=f(x₁，x₂，…，x_n)作为θ的估计量，即为参数θ的点估计。如果随机变量x的分布函数F(x；θ₁，…，θ_k)中有k个不同的未知参数，则要由子样x₁，x₂，…，x_n建立k个不带有任何未知参数的统计量作为这k个未知参数的估计量，常记作。

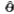鉴别估计量好坏的常用标准有：
❶ 无偏性：设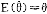是θ的估计量，当满足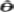时，称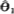为θ的无偏估计；
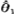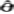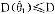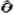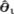❷ 有效性：若θ的某估计量对于除外任何其他的估计量均有()，则称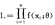为对θ最有效(具有最小方差)的估计量。

常用的点估计方法有：
❶ 矩估计法：即用子样矩作为总体矩的估计；
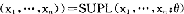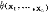❷ 最大似然估计法：由总体分布密度函数f(x；θ)，按样本观察值构造似然函数，选取使#成立的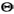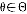作为θ的估计；
❸ 贝叶斯估计法：依赖于θ的先验分布的估计方法。

还有序贯估计法、最小平方估计法等。

设总体x的分布函数F(x；θ)中的θ为未知参数，由子样x₁，…，x_n建立两个统计量T₁(x₁，…，x_n)及T₂(x₁，…，x_n)，并满足T₁＜T₂，〔T₁，T₂〕为随机区间。

区间估计的表述为：设α为一给定常数(0＜α＜1)，若P{T₁≤θ≤T₂}=1－α成立，并用该随机区间作为θ的估计，则〔T₁，T₂〕是参数θ的置信水平为1－α的区间估计。α为显著性水平，T₁、T₂分别为上、下置信限。