自助法

---

利用样本数据本身得到有关经验估计量抽样特性的方法。

假定θ_n是由样本X=(X₁，…，X_n)得到的参数向量θ的估计量。要想得到θ_n具有统计特性的近似值，可以通过对自助性估计量θ(b)m加工得到，b=1，…，B。

首先从X中用随机抽样的办法对m个样本点有放回的取样，然后用每一个样本重新计算θ。(自助法样本容量m，有可能大于n也有可能小于n)这样共进行B次，就可以由

θ=[θ(1)m，…，θ(B)m]

计算出期望的抽样特征。

例如，如果知道估计量是连续的，样本容量n相当大，这时就可以用

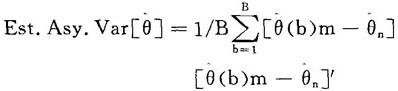
计算出估计量的θ渐进协方差矩阵的近似值。

近来自助法的应用越来越广泛，详情请参见Vinod & Raj(1994)，Veall(1987，1992)的文章。