自助法

---

是美国统计学家艾弗尨于1979年提出的一种处理非参数统计推断问题的方法。

如果设Y_n=(y₁，…，y_n)为来自母体(Y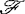，，F)的简单随机样本，F为一未知的分布函数，我们要解决的问题便是，对于某个特定的随机变量R(Y_n，F)，它可能依赖于Y_n和未知分布F，在Y_n观察值的基础上，估计R(Y_n，F)的抽样分布。

针对上面提出的问题，自助法就是：

(1)构造分布函数F的估计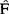，一般采用样本Yn的经验分布。

(2)给出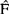后，从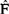中抽取容量为n的简单随机样本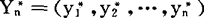，称为Bootstrap样本，其中。

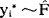(3)求出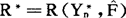在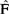下的分布，称为Bootstrap分布，然后利用R^*的Bootstrap分布作为R的抽样分布的近似。

Bootstrap过程的困难在于Bootstrap分布的实际计算，一般有三种可能的算法：

方法1．直接的理论性计算。

方法2．蒙特卡罗近似：

从F从中重复抽取N个样本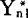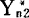，，Y，从而可以得到R^*的N个值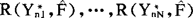，利用此N个值做直方图便可作为Bootstrap分布的近似。

方法3．δ－方法

对非线性的R(Y_n，F)进行泰勒展开，用线性部分或高阶多项式部分来近似R(Y_n，F)。

Bootstrap方法的本质就是用F的极大似然估计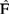来代表F，其中的蒙特卡罗算法对任何F都可以计算，正如艾弗龙所说的那样，“自助法是一种非常适应于现代这种有充分计算能力的时代的理论和方法”，自助法将会成为一种标准的统计方法。

自1979年以来，自助法得到了较大的发展，如自助法的渐近理论，自助法在回归分析时间序列分析方面的应用等。