蒙特卡罗方法

---

蒙特卡罗方法是指两种虽有紧密联系但却不同的方法。

第一种方法是用随机变量估计定积分。该方法的核心思想是，利用随机问题的解方法来推导出确定性问题的解。例如，假设要求定积分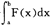F(x)dx(这里的x可以是向量)的值。可以通过估计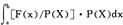[F(x)／P(X)]·P(X)dx来得到，式中的P(x)是某个定义在[a，b]上的随机变量的密度函数。

这样求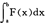F(x)dx的问题就转化成了求F(x)／P(X)的数学期望。可以通过从密度为P(X)的总体中抽样并计算F(x)／P(X)的平均值来解决这个问题。

第二种蒙特卡罗方法是指利用模拟数据来分析各种估计方法的小样本参数估计式的特性。该方法可分为以下六个阶段：

(1)设计研究模型

根据研究目的，设计模型形式，确定参数具体数值。

(2)模拟数据生成过程

建立计算机模拟数据生成过程的模型，模拟某种特定的现实数据生成过程。

这个模型常常根据所研究问题的特点进行设计，例如含测量误差的样本、多重共线性的样本、异方差性或序列相关性的样本。

这个模拟模型首先要给出随机扰动项的分布形式，一般选择期望为零，方差为有限值的正态分布。计算机模拟数据生成程序能够根据规定分布随机抽取n个随机扰动值，任意地给出先决变量的n个观测值，然后，可以根据规定的参数方程、选定的解释变量和随机扰动项数值，直接求出内生变量的值。

(3)生成数据

将数据生成过程的模型输入计算机，就可以生成任意数据。根据需要，可以确定样本容量n，例如n=40，还要确定反复抽样的次数m，例如m=1600。

(4)计算参数估计值

利用各种方法的参数估计式以及上面抽取的m个样本，可以计算参数估计值。

(5)估计参数的抽样分布

利用上述参数样本，可以计算参数样本统计量，如：期望值、方差、均方差等。

(6)比较参数估计式特性

根据上面的研究成果，可以比较不同的估计方法的参数估计式特性，给实际的经济计量分析提供依据。