虚数

---

形如bi的数，其中b是实数，i是“虚数单位”(i²=－1)。

虚数并不“虚无”，它是在解决有关生产实践中提出的代数方程中产生的，是实数在一定条件下转化的结果。16世纪30年代，意大利数学家卡尔丹诺(Cardano，G．)在解三次方程的求根公式中引用了负数开平方表示实系数方程的根。虚数单位i是在1777年由欧拉首先引用的，但直到1801年高斯系统地使用这个符号，才渐渐通行于全世界。

虚数与实数是对立统一的，在一定条件下相互转化。

例如，实数－1在开平方运算下转化成虚数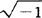=i，而虚数i=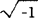在平方运算下转化为实数－1。在此基础上建立了一系列合理运算法则，为研究二、三次方程开创了新局面。此后虚数便被人们逐渐认识。虚数bi与实数a的复合形式a+bi称作复数。

这样，虚数与实数在复数系统中统一起来了。18世纪末、19世纪初，复数才有了直观的几何表示，虚数也有了与实际内容相联系的解释。

反过来，复数及复数理论的形成与发展又推动了数学分析中的一个重要分支——“复变函数论”的迅速发展，它在许多学科尤其是流体力学中有著十分广泛和重要的应用。虚数归根结底是从实践中产生出来，但它又不是从生产实践中直接总结出来的，是在探讨方程的解法中从实数系中推导出来的正确数学运算的必然结果。

对虚数i本身不能硬加上在我们头脑以外的实在性，它以极度抽象的形式出现只能在表面上掩盖它起源于外部世界的事实。