证券市场线

---

如图1，以证券组合的预期收益率r_p作纵坐标，以证券组合的标准差δ_p作横坐标，绘出证券组合的可行集和资本市场线。

在可行集里，存在各种单一风险证券，任意选择一种证券，用i表示。设想一证券组合，用P表示，它包含证券i的投资比例是X_i，市场证券组合的投资比例是(1－X_i)，这种证券组合的预期收益率等于：

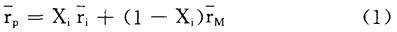
和标准差等于：

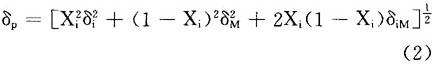
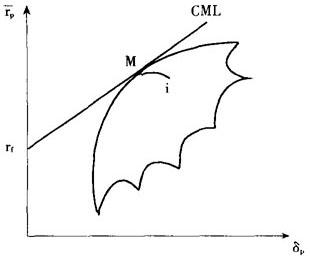
图1 推导证券市场线

首先在(1)中，求r_p对X_i的导数：

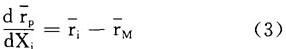
其次在(2)中，求δ_p对X_i的导数：

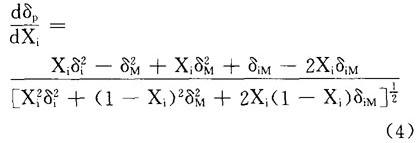
再次，考虑曲线iM的斜率，有如下表达形式：

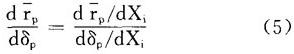
最后，把(3)和(4)分别代入(5)：

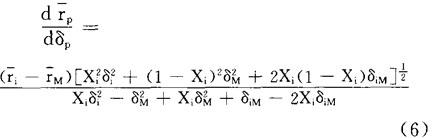
在曲线iM的端点M处，X_i=0，可计算出曲线iM的端点M处的斜率：

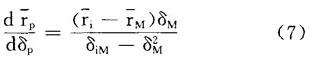
在点M处，资本市场线的斜率必然等于曲线iM的斜率，因此

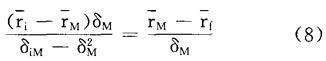
解方程(8)，#_i等于：

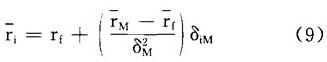
它表明了单一一种证券资产的风险和收益率之间的均衡关系，分别以证券的协方差风险δ_i和预期收益率r_i为横坐标和纵坐标，在图2－a中，方程(9)代表具有截距r_f和斜率[(rM－r_f)／δ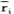]的一条直线，证券的协方差风险δ_iM和预期收益率之间的这种关系称为证券市场线。

证券市场线的另一种表达方式如下：

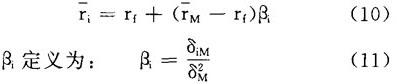
β_i项称为证券i的β系数，它代表一种证券的协方差风险。

如果以证券的预期收益率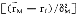_i为纵坐标，以β_i为横坐标，则证券市场线也可以表现在图2－b中。

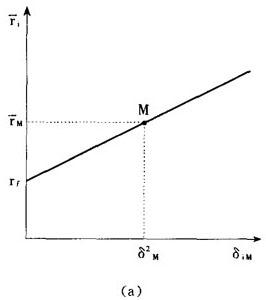
图2－a 协方差观点

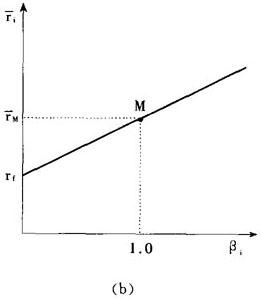
图2－b β观点