非线性规划、库恩－塔克定理

---

非线性规划是在约束g_i(x₁，x₂，…，x_n)≦b_i(i=1，…，m)之下，求x=(x₁，x₂，…，x_n)使目标函数f(x₁，x₂，…，x_n)最大化的问题，其中g_i和f中至少有一个不是线性函数，而且g_i和f均一次连续可微。

如果所有的约束都是等式，即g_i(x₁，…，x_n)=b_i，(i=1，…，m)，则可用拉格朗日(Lagrange)乘数法求解。构造拉格朗日函数L(x，λ)=f(x)－#λ_i(g_i(x)－b_i)，其中x=(x₁，…，x_n)，λ=(λ₁，…，λ_m)。f(x)在x^*取最大值的必要条件将是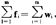|x^*=0，(j=1，…，n)。

可解这个方程组求出x^*。

如果约束不全为等式，而且从经济意义考虑要求x_j(j=1，…，n)为非负，则有如下的库恩－塔克定理：如果g_i(x)(i=1，…，m)满足约束品性条件，则在g_i(x)≦b_i(i=1，…，m)和x_j≧0(j=1，…，n)的约束下，f(x)在x^*取最大值的必要条件是存在λ₁，λ₂，…，λ_m满足：

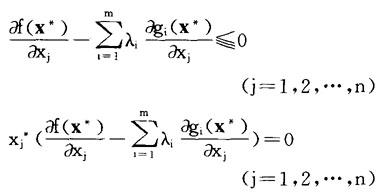
g_i(x^*)≦b_i，λ_i(g_i(x^*)－b_i)=0，

λ_i≧0 (i=1，2，…，m)

x_j≧0 (j=1，2，…，n)

约束品性条件有好几种形式，其中之一是斯拉特(Slater)条件，它要求存在一个点x°≧0，满足g_i(x°)＜b_i(i=1，2，…，m)，即在x°处所有约束均是严格的不等式。

可以证明，x^*和λ₁，…，λ_m满足关系λ_i=，(i=1，2，…，m)。

如果把x看成生产活动水平，g_i(x)是第i种资源的消费量，b_i是它的最大可能利用量(资源存量)，目标函数f(x)是对应于活动水平x的收益，则λ_i就是第i种资源存量增加一单位时最大收益的增量，因此λ_i就是第i种资源的影子价格。

参见"影子价格"。