函数项级数　一致收敛性

---

函数项级数的一般概念

(1)设函数列u₁(x)，u₂(x)，…，u_n(x)，…中每一个函数都在区域I内有定义，则

称为定义在I内的函数项级数，简称函数项级数．

(2)若x₀∈I使数项级数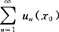收敛，则称x₀为函数项级数的收敛点．收敛点的全体叫做函数项级数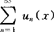的收敛域．

(3)和函数定义

设函数项级数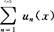的收敛域为G．则G上就有一个函数S(x)，使

此函数称为函数项级数的和函数．

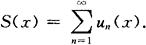
函数项级数的一致收敛(或称均匀收敛)定义 设函数项级数的和函数为S(x)，(x属于收敛域内)．如果对于任意给定正数ε，存在相应的正整数N，当n＞N时，不等式

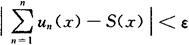
在某个区间I内对任何x均成立，则称函数项级数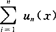在I内一致收敛．

魏尔斯特拉斯(Weierstrass)定理 设函数项级数在某区间I内恒有|u_n(x)|≤Mn(n=1，2，…，x∈D．且正项级数收敛，则函数项级数在该区间内I一致收敛，且绝对收敛．

正项级数称为函数项级数的优势级数．

一致收敛级数的基本性质

(1)设函数项级数中每一项函数u_n(x)(n=1，2，…)在区间(a，b)内连续，且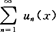在(a，b)内一致收敛于和函数S(x)，则S(x)在(a，b)内连续．

(2)设级数中每一项函数u_n(x)(n=1，2，…)在［a，b］上连续，且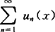在［a，b］上一致收敛于S(x)，则其和函数S(x)在［a，b］上可积，且有

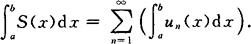
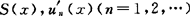(3)设级数在区间(a，b)内收敛于和函数在(a，b)连续且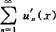在(a，b)内一致收敛，则级数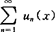在(a，b)内一致收敛，其和S(x)在(a，b)内有连续的导数，且