一元线性回归
一元线性回归yiyuan xianxing huigui
一元线性回归是工程上和科研中常常遇到的配直线问题,即两个变量X和Y有一定的线性关系,通过试验,利用得到的数据找出两者之间的经验公式。
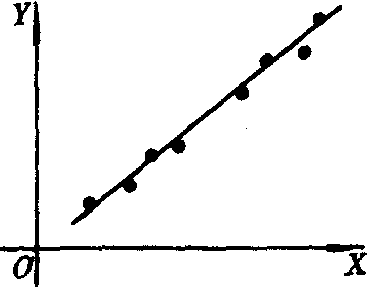
为了寻求变量X和Y之间的关系,我们对 (X,Y)作n次独立观察,获得n对观察值(xi ,yi)(i=1,2,…,n),再以它们为坐标,在坐标平面上描出n个观察点,如果这n个观察点分布在一条直线近旁(如图),则这条直线即可代表x与y之间的关系.下面利用最小二乘法来求此直线的方程。
设直线的方程为
 =a +bX
=a +bX
 i) 之间的偏差为
i) 之间的偏差为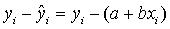
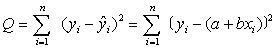
求回归直线的方程
 =a+bx,并归结为求a, b使Q达到最小值。
=a+bx,并归结为求a, b使Q达到最小值。求Q关于a与b的偏导数,并令它等于零得
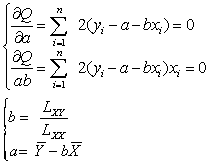
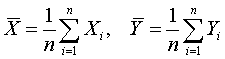
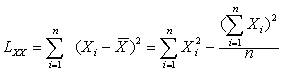
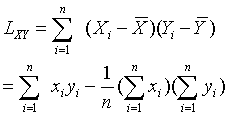
Y=a +bX。
注意,只有当两个变量之间确实存在线性统计关系时,求出的回归直线方程才有意义。
☚ 最小二乘法 微积分 ☛
一元线性回归
一元线性回归
因变量y与一个自变量x之间有线性关系, 其关系式为ŷ=b0+b1x, b0为直线截距,b1为斜率,即回归系数。根据样本资料,用最小二乘法去估计b0和b1,有正规方程组:
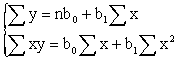
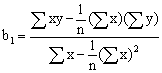
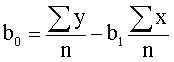
☚ 非线性回归 多元线性回归 ☛
- 围索索是什么意思
- 围绕是什么意思
- 围绕“周末”这个话题是什么意思
- 围绕“感受生活”这个话题是什么意思
- 围绕“我·未来”联想想象作文是什么意思
- 围绕“换位”这个话题是什么意思
- 围绕“文学的启迪”这一话题是什么意思
- 围绕与地球有关的内容是什么意思
- 围绕国大的纵横捭阖是什么意思
- 围绕在坦克车等的车轮上的钢质链带是什么意思
- 围绕在城门外的小城是什么意思
- 围绕对华军事援助的交涉是什么意思
- 围绕市场的垣墙是什么意思
- 围绕帝王或侯国宫室院落的城垣是什么意思
- 围绕总统大选的各方博弈是什么意思
- 围绕悉栴檀,纯良岂沙砾。是什么意思
- 围绕某一中心运行是什么意思
- 围绕田或屋的防水堤是什么意思
- 围绕的样子是什么意思
- 围绕着做圆周运动是什么意思
- 围绕着联合政府问题的国共谈判是什么意思
- 围绕绵长是什么意思
- 围绕选举副总统问题上的斗争是什么意思
- 围绕高山平原是什么意思
- 围绝经期综合征是什么意思
- 围网是什么意思
- 围网作业是什么意思
- 围网捕捞是什么意思
- 围网捕捞机械是什么意思
- 围网探鱼船是什么意思
- 围网渔船是什么意思
- 围网甲板艇是什么意思
- 围网绞机是什么意思
- 围网船是什么意思
- 围网起网机是什么意思
- 围罗是什么意思
- 围羞带减是什么意思
- 围老虎是什么意思
- 围而不打是什么意思
- 围而不打,隔而不围是什么意思
- 围而不攻是什么意思
- 围而不攻取野王是什么意思
- 围聚是什么意思
- 围肚儿是什么意思
- 围肚子是什么意思
- 围脖是什么意思
- 围脖儿是什么意思
- 围脖子是什么意思
- 围脖手绢是什么意思
- 围腰是什么意思
- 围腰儿是什么意思
- 围腰子是什么意思
- 围腰帕是什么意思
- 围腰带剩是什么意思
- 围腰得是什么意思
- 围腰花的来历是什么意思
- 围腾是什么意思
- 围范是什么意思
- 围药是什么意思
- 围蛹是什么意思