均衡的惟一性、稳定性uniqueness,stability of equilibrium

在一般均衡分析中，设Z_i(p)=D_i(p)-S_i(p)为第i种商品的超需函数，则均衡价格p就是使Z_i()=0,(i=1,2，…，n)的向量。 如果存在一个p能满足这个方程组，是否还有别的p也能满足它呢？这就是均衡的惟一性问题。
常见的惟一性定理基于泛替代性(gross substitutes)假设，对两种商品i和j，如果当i≠j时必有∂Z_j;(p)/∂p_i>0，则称i和j在价格p上有泛替代性。当所有不同商品之间都有泛替代性时，可以证明，如果p为均衡，则它必惟一。
均衡稳定性是研究当价格向量p₀≠时，随着时间的推移，从p₀出发的价格轨道p是否会收敛于p的问题。
瓦尔拉斯把非均衡价格收敛到均衡价格的过程设想为一个价格调整过程(参见“摸索过程”)，萨缪尔森把这个思想表达为下述微分方程组：

其中k_i是正常数，称为调整速度。
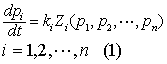
由于在均衡价格处有Z_i()=0,i=1,2，…，n，故就是微分方程组(1)的平衡解。对于定义域中任意的初始价格p₀≠p，如果当t→∞时有p(p₀,t)→，则称均衡为全局（渐近）稳定的；如果对p存在一个邻域，从此邻域内的任一个p₀≠p出发的轨道，当t→∞时有p(p₀,t)→则称均衡p为局部稳定的。
把Z_i(p)在附近展开，略去二次以上的高阶项得近似的线性微分方程组

其中
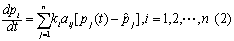
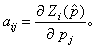
方程组(2)的均衡p为稳定的必要充分条件是矩阵A=[a_ij]的所有特征值均有负实部。由(2)的稳定性可得到(1)的局部稳定性。关于(1)的全局稳定性有结果：如果对所有p≠，有·z(p)>0，则均衡是全局稳定的。