契比雪夫不等式qibixuefu budengshi

设01≤

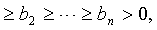
则

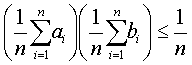
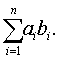
如果

或

则

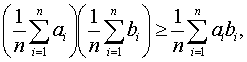
当a1＝a2＝…=an

且

b1＝b2＝…=bx

时各式取等号.

更一般地，若

01≤a2≤…≤ax,01≤b2≤…≤

bx或a1≥a2≥…≥ax>0,b1≥b2≥…≥bx>0,r>0

则

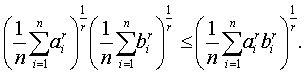
如果

a1≥a2≥…≥ax>0,01≤b2≤…≤bx

或

01≤

a2≤…≤ax, b1≥b2≥…≥bx>0, r>0

则

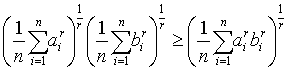
当

a1=a2

=…=ax

且

b1＝b2=…=bx

时各等式取等号.

＝…=a_n且b₁＝b₂＝…=b_n时各等式取等号.

☚ 贝努利不等式 　 赫尔德不等式 ☛

---

契比雪夫不等式qibixuefu budengshi

设随机变量X的期望E (X)与方差D (X)存在，则对任意的ε>0，有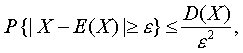或P{|X-E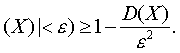
这就是著名的契比雪夫不等式，契比雪夫不等式给出了在未知X的分布情况下，对概率P {|X-E(X) |≥ε) 或P {|X-E (X) |<ε) 的一种估计，这种估计只需要知道方差D (X)及数学期望E (X)两个数字特征就够了，因而，使用起来较为方便，但是，它没有完整地用随机变量的统一规律——分布函数或密度函数，因此，一般地说，由此不等式给出的估计是比较粗的，例如，若X是N (α,σ2)分布的随机变量，则由不等式得估计

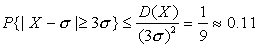
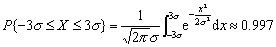而由可知P {|X-α|≤3σ) ≈0. 997，故有P {|X-α|≥} 3σ≈0. 003，从这两个结果可以看出，契比雪夫不等式给出的估计是较为粗的，然而，它在理论上有重要意义，

☚ 常见随机变量的期望与方差 　 大数定律 ☛