两圆相切的性质

---

如果两圆相切，那么两圆的连心线必经过切点．

注意 已知条件中有两圆相切时，常常过切点作两圆的公切线，这是圆中常添加的辅助线．

例1 如图，☉O和☉O′内切于P点，半径OA和OB切☉O′于C，D，连O′C和O′D，如果两圆半径分别为9和3，求∠CO′D的度数．

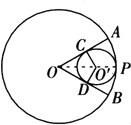
解 ∵☉O与☉O′内切于P点，所以连接OO′并延长必过切点P．

∵OA切☉O′于C点，

∴O′C⊥OA．

同理O′D⊥OB．

∵O′C=O′D，

∴OO′平分∠AOB．(角平分线性质定理的逆定理)

在Rt△OO′C中，O′C=3，OO′=9－3=6．

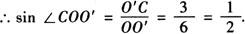
∴∠COO′=30°．

∴∠COD=60°．

在四边形ODO′C中

∵∠O′CO=∠O′DO=90°，

∴∠CO′D=120°．

例2 两圆半径分别为2cm，3cm，圆心距为5cm，两圆公切线的条数为( )．

A．1条 B．2条

C．3条 D．4条

答 C．

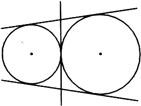
[解析] 两圆外切共有3条公切线，两条外公切线和1条内公切线．

两圆内切只有一条内公切线，如图所示：

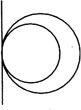
例3 如图，已知：☉O₁与☉O₂外切于P点，AB分别切☉O₁、☉O₂于A、B两点．

求证：PA⊥PB．

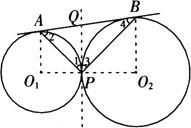
证明 连接O₁O₂．

∵☉O₁与☉O₂外切于P点，

∴O₁O₂必过P点．

连接O₁A、O₂B，过P点作☉O₁与☉O₂的内公切线交AB于Q点．

∴∠O₁AQ=∠O₁PQ=∠O₂BQ=∠O₂PQ=90°．

又∵O₁A=O₁P，O₂B=O₂P，

∴∠O₁AP=∠O₁PA，∠O₂BP=∠O₂PB．

∴∠1=∠2，∠3=∠4．

∴∠1+∠3=∠2+∠4．

又∠1+∠2+∠3+∠4=180°．

∴∠1+∠3=90°．

即PA⊥PB．

[解析] 两圆外切且有一条外公切线，三个切点构成的切点三角形为直角三角形．

例4 如图两圆外切于点T，AB是外公切线，切点分别是A、B，连心线O₁O₂交两圆于C、D，CA、DB的延长线交于点E，求证四边形ATBE是矩形．

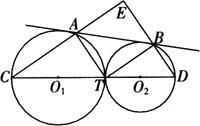
证明 ∵CT为☉O₁直径，∴∠CAT=90°．

同理∠DBT=90°．

由例3可知∠ATB=90°．

∴在四边形ATBE中，∠EAT=∠A7B=∠EBT=90°．

∴四边形ATBE为矩形．