极大似然法
设f(x,θ1,θ2,…,θr)为随机变量ξ的密度函数,其中θ1,θ2,…,θr为未知参数,构造θ1,θ2,…,θr的似然函数L(θ1,θ2,…,θr),在使该似然函数极大的条件下估计未知参数θ1,θ2,…,θr的方法称为极大似然法。常被应用于测验分数统计中。
极大似然法
极大似然法
极大似然法是对总体参数θ作点估计的一个较好方法。 其优点是用它来求得的参数估计量 常能满足一致性和有效性等要求,并且具有不变性。 不变性指当
常能满足一致性和有效性等要求,并且具有不变性。 不变性指当 为θ的极大似然估计量时,则二者任何同一函数变换值,仍保持这种关系,比如lg
为θ的极大似然估计量时,则二者任何同一函数变换值,仍保持这种关系,比如lg  仍是lg θ的极大似然估计量。应用本法的前提是已知总体的分布,而未知其参数。对离散型分布,要已知概率函数p(X);对连续型要已知密度函数f(X)。本法是以从总体中抽得现有样本的可能性为最大的这一原则来确定参数的估计值。这里的可能性为最大也就是似然函数L(θ)为极大。
仍是lg θ的极大似然估计量。应用本法的前提是已知总体的分布,而未知其参数。对离散型分布,要已知概率函数p(X);对连续型要已知密度函数f(X)。本法是以从总体中抽得现有样本的可能性为最大的这一原则来确定参数的估计值。这里的可能性为最大也就是似然函数L(θ)为极大。
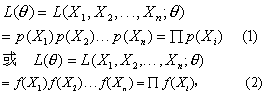
式中X1,X2,…,Xn是含量为n的样本。未知参数可以是一个,如θ;也可以是k个,如θ1,θ2,…,θk。
根据数学分析方法,当L(θ)的极大值存在时,将L(θ)对θ求一阶导数使之等于零,解得的能使L(θ)为极大的θ值,即
 ,这样求
,这样求 的方法称为极大似然法。
的方法称为极大似然法。例1 设一个含量为n的随机样本取自点二项分布的总体:
p(X)=πX(1-x)1-x,X=0、1,0≤π≤1。
求参数π的极大似然估计量。
按式(1),得似然函数及其自然对数为
L(π) =π∑Xi (1-π)n-∑Xi,ln L(π)=∑Xilnπ+(n-∑Xi) ln(1-π)。
求上式的导数,并使之等于零,
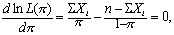
解之,得π的极大似然估计量为
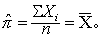
若总体的阳性率为π,当试验结果为阳性时,X=1;为阴性时,X=0。如果在n次试验中有k次为阳性,则∑Xi=k,于是
 =k/n=p。 即π的估计量为样本率p。例2 设X服从正态分布N(μ,σ2),求未知参数μ与σ2的极大似然估计量。
=k/n=p。 即π的估计量为样本率p。例2 设X服从正态分布N(μ,σ2),求未知参数μ与σ2的极大似然估计量。正态分布的密度函数为
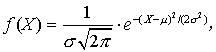
设X1 ,X2,…,Xn为所得样本的观察值,按式(2)得似然函数及其自然对数为
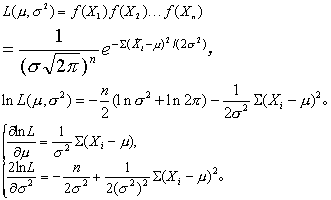
令此导数为零,并解之:
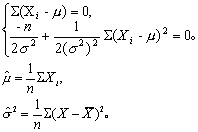
这便是μ与σ2的极大似然估计量。根据它的不变性,得
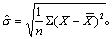
☚ 参数的点估计 可信区间 ☛
极大似然法
极大似然法maximum-likelihood method
求未知参数点估计的方法。劳利1940年提出。尤洛斯格等人1967年提出一个较为实用的计算方法后得到广泛使用。基本思想是,设已知一随机试验有若干不同结果A,B,C,…,如果在一次具体试验中A发生了,则可认为当时条件最利于A发生,故应选择使A发生概率最大的分布的参数。具体过程就是构造一个以观测值和未知参数为自变量的似然函数,并通过极大化此似然函数,从而获得模型的参数估计。
☚ 点估计 区间估计 ☛
- 君子曰:学不可以已。青,取之于蓝,而青于蓝;冰,水为之,而寒于水。是什么意思
- 君子曰:礼乐不可以斯须去身。是什么意思
- 君子有三乐是什么意思
- 君子有三乐,而王天下不与存焉。父母俱存,兄弟无故;一乐也。仰不愧于天,俯不怍于人,二乐也。得天下英才而教育之,三乐也。是什么意思
- 君子有三变:望之俨然,即之也温,听其言也厉。是什么意思
- 君子有三忧:弗知,可无忧与?知而不学,可无忧与?学而不行,可无忧与?是什么意思
- 君子有三患五耻是什么意思
- 君子有三患:未之闻,患弗得闻也;既闻之,患弗得学也;既学之,患弗能行也。是什么意思
- 君子有三戒是什么意思
- 君子有三戒:少之时,血气未定,戒之在色;及其壮也,血气方刚,戒之在斗;及其老也,血气既衰,戒之在得。是什么意思
- 君子有三言可贯而佩之:一日无内疏而外亲;二日身不善而怨他人;三日患至而后呼天。是什么意思
- 君子有三言可贯而佩之:一曰无内疏而外亲,二曰身不善而怨他人,三曰患至而后呼天。是什么意思
- 君子有三鉴:鉴乎前,鉴乎人,鉴乎镜是什么意思
- 君子有不战,战必胜矣是什么意思
- 君子有主善之心, 而无胜人之色, 德足以君天下, 而无骄肆之容, 行足以及后世, 而不以一言非人之不善。是什么意思
- 君子有九思是什么意思
- 君子有五美是什么意思
- 君子有信。是什么意思
- 君子有勇而无义为乱,小人有勇而无义为盗是什么意思
- 君子有大道,必忠信以得之,骄泰以失之。是什么意思
- 君子有天下之私,小人有一身之公。是什么意思
- 君子有失其所兮,小人有得其时。是什么意思
- 君子有容人之量是什么意思
- 君子有常交, 曰义也; 有常誓, 曰信也。是什么意思
- 君子有徽猷,小人与属是什么意思
- 君子有教,则人皆可以复于善,而不当复论其类之恶矣。是什么意思
- 君子有机以成其善,小人有机以成其恶是什么意思
- 君子有机以成其善,小人有机以成其恶。是什么意思
- 君子有礼,则外谐而内无怨也。是什么意思
- 君子有礼,外谐内无怨是什么意思
- 君子有絜矩之道。是什么意思
- 君子有终身之忧,无一朝之患是什么意思
- 君子有自反之道是什么意思
- 君子有自反之道,无求人之理是什么意思
- 君子有诸己而后求诸人是什么意思
- 君子有诸己而后求诸人,无诸己而后非诸人。所藏乎身不恕而能喻诸人者,未之有也。是什么意思
- 君子有过不辞谤,无过不反谤,共过不推谤。谤无所损于君子也。是什么意思
- 君子有远虑,小人从迩是什么意思
- 君子有通财之义是什么意思
- 君子树是什么意思
- 君子欲利而不为非。是什么意思
- 君子欲纳于言,而敏于行。是什么意思
- 君子欲言之见信也, 莫善乎先虚其内。是什么意思
- 君子正身以俟,欲来者不距,欲去者不止。是什么意思
- 君子比德于玉是什么意思
- 君子比莲花(打聊目一)王六郎是什么意思
- 君子求诸己,小人求诸人是什么意思
- 君子求诸己,小人求诸人。是什么意思
- 君子法之以昭明德是什么意思
- 君子泰而不骄。是什么意思
- 君子泰而不骄,小人骄而不泰是什么意思
- 君子津是什么意思
- 君子济困不济富是什么意思
- 君子济贫不济富是什么意思
- 君子淡以亲,小人甘以绝是什么意思
- 君子淡以亲,小人甘以绝。是什么意思
- 君子淡如水,岁久情愈真;小人口如蜜,转眼成仇人是什么意思
- 君子爱人以德是什么意思
- 君子爱人以德,小人爱人以姑息是什么意思
- 君子爱惜人才,小人排挤异类是什么意思