样本方差yangben fangcha

样本数据离散度的较精确的表示是用每个样本数据偏离其中心位置的大小来表示。这里的中心位置一般用样本均值表示，而每个数据xi偏离的大小则用离差x_i-的平方来表示。于是，全部n个数据的离差平方和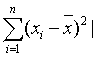即可用来表示样本数据的离散程度，为了消除样本大小n的影响，我们将离差平方和除以n-1所得的商

称为样本方差，它的算术平方根

称为样本的标准差。
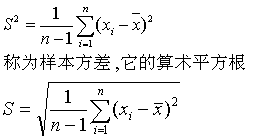
采用样本标准差的原因之一是它的量纲与数据的量纲一致，在实际使用中较为方便。
由于n个离差x_i-的总和一定等于0，即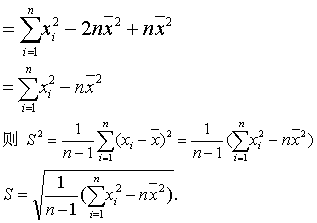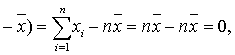这n个离差中相互独立的个数只有n-1，而不是n。因此，我们在样本方差和样本标准差的定义中，用n-1而不是用n作除数，n-1通常称为样本方差或标准差的自由度。
例如，设某种产品的一种性能的合格范围是160～175cm，下面是甲、乙、丙三个工人生产的这种产品的性能记录，试比较他们的技术水平。
甲： 166,164,167,165,1.68,169,170,167。
乙： 171,178,182,167,153,152,161,172。
丙： 191,190,167,150,197,154,144,143。
经计算，三组数据的平均值均为167，其方差、标准差分别为：
S²_甲＝4,S_甲＝2; S²_乙＝120.57,S_乙＝10.98; S²_丙＝509. 71,S_丙＝22. 57。
由此可知，甲的技术水平最稳定，其次是乙，最次的是丙。
总体方差是指总体的数量指标X的方差，即D(X)，总体标准差是指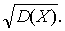。总体方差是一个非负实数，而样本方差是一个随机变量，两者有根本差别。

样本方差sample variance

与“总体方差”相对。样本数据的方差。用S²表示。当总体方差未知，需要对其进行估计时，通常使用样本方差的修正公式估计总体方差，以保证估计的无偏性。