泊松分布Poisson distribution

概率论中近似于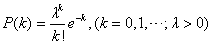的一种概率分布。泊松分布的均值为λ,k为样本数。由法国数学家泊松(S.D.Poisson,1781～1840)首先提出，故名。它大量出现于社会生活和物理现象中。如来到车站的乘客数、放射线照射诱导的突变率、显微镜下落在某视野中的血球或微生物数等，都服从泊松分布。

泊松分布bosong fenbu

设随机变量X的可能取值为0,1,2，…，且

其中，λ>0为常数，则称X服从参数为λ的泊松分布.
泊松分布可作为描述大量试验中稀有事件出现频数k的概率分布的数学模型，它是一种重要的概率分布.
对二项分布B (n,p)来说，若n充分大，p相对很小，则

其中λ=np.因此，当n充分大时，二项分布B(n,p)可近似地看作以λ=np为参数的泊松分布.

泊松分布

一种常用的重要的概率分布。在社会科学、物理学等方面许多随机现象服从泊松分布。例如在长度为t的时间间隔中某电台的电话呼叫次数为k的概率是Pk(t)=e-(k=0,1，…),λ是常数，这就是泊松分布的具体形式。

泊松分布Poisson distribution

是数理统计中属于离散型变量分布，常用来说明随机现象的分布特点。条件是当某种事件出现的概率很小(P <0.01)，而样本含量又很大时，则其二项分布即逐渐逼近泊松分布。其概率函数为：

式中x为随机变量，x=0,1,2，…λ为总体均数，0≤λ<∞,! 为阶乘符号，e为自然对数的底，e=2.71828。医学研究中常使用泊松分布来说明某些小概率事件的随机离散特征，如检验某种恶性肿瘤发病有否集聚性，即可采用泊松分布来判断，如判断不符合泊松分布，即证明该肿瘤无集聚性。

泊松分布Poisson Distribution

亦称“普阿松分布”。统计与概率学中常见的离散概率分布。由法国数学家德尼·泊松于1838年提出。若随机变量 X 只取非负整数值，取k值的概率为P(X=k)=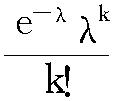(k=0,1,2，…), 则随机变量X 的分布称为泊松分布，记作P(λ)。泊松分布P (λ)中参数λ既是泊松分布的均值，也是泊松分布的方差。

泊松分布

利用二项分布时，常常遇到这种情况，即P非常小(在0.1以下)，而n较大(在500以上),np在0～10之间)np称为泊松分布的平均值)。在这种情况下，研究诸如“次品率为1%的产品，每箱装100个时，求一箱中次品为零(或2个的概率”的问题时，使用下面的公式（泊松公式）更为方便。

式中：f(k)为发生k次事件的概率，λ=np在实用中往往代表一定单位内的缺陷数，e为自然对数的底，泊松分布可看做是二项分布的一部分，因为变量k只取正整数和零。纺织品的疵点，电镀表面的麻点等计点数值的概率基本符合泊松分布。

泊松分布Poisson distribution

亦译“普阿松分布”。离散分布的一种。描述单位时间内随机事件发生次数的概率分布。由法国数学家泊松(Siméon Denis Poisson, 1781—1840)1838年发表。函数表达式为： P(x=k)=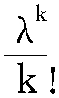e^-λ(k=0, 1, 2…)，其中参数λ是单位时间（或单位面积）内随机事件的平均发生率。如某一商场在一定时间内顾客数，公交站台候客人数，机器出现故障数，地质灾害发生次数等。泊松分布在管理学、运筹学以及自然科学特定问题中都得到重要应用。