球面qiú miàn

半圆以直径为轴旋转而形成的曲面；球的表面。1855年6月《遐迩贯珍》第六号：“地理书每说球面方位离赤道之多少，必云某方阔处有北度若干或南度若干。”1855年合信《博物新编》二集《仿做地球经纬法论》：“球面中画一横带，带之上名北半球，带之下名南半球。”

球面qiumian

半圆以它的直径为轴旋转所成的旋转面.
球面也可以看作空间与定点的距离等于定长的所有点的集合（轨迹）.

---

球面qiumian

与一定点的距离是定长的空间点的轨迹。此定点叫球心，定长叫半径。以P₀ (x₀,y₀,z₀)为球心，r为半径的球面方程的 向量形式为|P-P₀|=r。坐标形式为 (x-x₀)²+ (y-y₀)²+ (z-z₀)²＝r²。球面方程的一般形式也可以写成x²+y²+z²+2ux+2vy+ 2wz+d= 0。三元二次普遍方程ax²+by²+cz²+2fyz+2gzx+2hxy+2ux+2vy+ 2wz+d=0表示一个球面的充要条件是a=b=c≠0,f=g=h=0,u²+v²+w²-ad> 0。球心是(-u/a,-v/a,-w/a)，半径是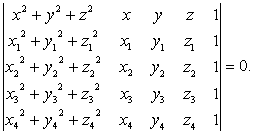当u²+v²+w²-ad= 0时，则表示一个点(-u/a,-v/a,-w/a)，当u²+v²+w²-ad<0时，则没有实轨迹。已知四个不共面的点P_i (x_i ,y_i,z_i)(i=1,2,3,4)，过此四点的球面方程是

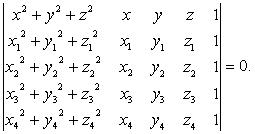
球面Qiumian

曲面的一种，指球体表面的形态而言，是曲线做圆周运动的轨迹。球面的特征表现为多向的起伏变化，是曲面中变化比较丰富的一种。球面还可以分为正圆球面、椭圆球面和卵形球面等几种类型。正圆球面的起伏变化，在各个方向上都是相同的，是球面中最单纯的形式。椭圆球面和卵形球面，在不同方向上变化则有所不同。球面是陶瓷造型中运用最多的一种，因为与可塑性的材料和成型方式有关系，以及这种球面在力学上的特点，一直成为造型主要的形式。

球面

spherical surface;surface of a sphere