等差数列←→等比数列děng chà shù liè ← → děng bǐ shù liè
等差数列:由第二项起,任一一项与前一项的差恒等的数列,如:7、10、13、16
等比数列:由第二项起,任一项与前一项的比恒等的数列,如:3、6、12、24
等差数列
等差数列dengcha shulie
从第二项起,每一项都等于前一项加上同一个数d的有限数列或无限数列.又叫算术数列.这个数d称为等差数列的公差.等差数列可以记作
a1,a1+d,a1+2d,…,a1+(n-1)d,…
等差数列的通项公式是an=a1+(n-1)d
前n项和公式是
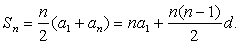
等差数列从第二项开始每一项是前项和后项的算术平均数.
如果等差数列的公差是正数,则该等差数列是递增数列;如果等差数列的公差是负数,则该数列是递减数列;如果等差数列的公差等于零,则该数列是常数列.
对于一个数列al,a2,…,an,…,如果它的相邻两项之差a2-a1,a3-a2,…,an+1-an,…构成公差不为零的等差数列,则称数列{an}为二阶等差数列.
运用递归的方法可以依次定义各阶等差数列:对于数列{an},如果{an+1-an}是r阶等差数列,则称数列{an}是r+1阶等差数列.二阶或二阶以上的等差数列称为高阶等差数列.
r阶等差数列的通项公式可以用一个关于项数n的r次多项式来表示,反之,通项公式为项数n的r次多项式的数列必为r阶等差数列.
高阶等差数列的求和方法主要有两种,一种是将其通项(项数n的r次多项式)表成差分多项式的线性组合从而求和.另一种是利用自然数幂的求和公式,如
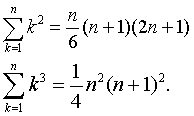
r阶等差数列的前n项和公式是项数n的r+1次多项式,对r不太高的情况也可用待定系数法来确定.
二阶等差数列的通项
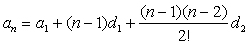
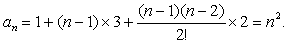
| 二阶等差数列前n项和 |
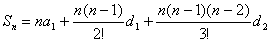
| 例如二阶等差数列 {n2}前n项和 |
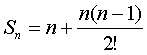
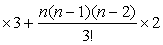
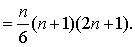
☚ 斐波那契数 高阶等差数列 ☛
- 中学校长是什么意思
- 中学校长实名推荐制是什么意思
- 中学校长实名推荐制是什么意思
- 中学模范作文辞典是什么意思
- 中学毕业会考是什么意思
- 中学毕业文凭是什么意思
- 中学气象活动组是什么意思
- 中学气象观测仪器是什么意思
- 中学汉英词典是什么意思
- 中学汉语倒序词典是什么意思
- 中学物理实用辞典是什么意思
- 中学物理实验手册是什么意思
- 中学物理手册是什么意思
- 中学物理教学改革试行方法是什么意思
- 中学物理教学研究常用方法是什么意思
- 中学物理教学词典是什么意思
- 中学物理教师手册是什么意思
- 中学物理教材体系结构研究技能是什么意思
- 中学物理概念·定律·公式大全是什么意思
- 中学物理演示实验大全是什么意思
- 中学物理百科第一分册——力学是什么意思
- 中学物理知识之最是什么意思
- 中学物理知识手册是什么意思
- 中学物理简明手册是什么意思
- 中学物理解题大全是什么意思
- 中学物理解题指南是什么意思
- 中学物理解题辞典是什么意思
- 中学班主任实用手册是什么意思
- 中学班主任工作手册是什么意思
- 中学班主任工作评价量表是什么意思
- 中学班主任手册是什么意思
- 中学理科基础知识手册是什么意思
- 中学生是什么意思
- 中学生优秀作文大全是什么意思
- 中学生体育协会是什么意思
- 中学生体育合格标准试行办法是什么意思
- 中学生作文借鉴1是什么意思
- 中学生作文借鉴10是什么意思
- 中学生作文借鉴11是什么意思
- 中学生作文借鉴12是什么意思
- 中学生作文借鉴2是什么意思
- 中学生作文借鉴3是什么意思
- 中学生作文借鉴4是什么意思
- 中学生作文借鉴5是什么意思
- 中学生作文借鉴6是什么意思
- 中学生作文借鉴7是什么意思
- 中学生作文借鉴8是什么意思
- 中学生作文借鉴9是什么意思
- 中学生作文借鉴小百科是什么意思
- 中学生作文借鉴辞典是什么意思
- 中学生作文典是什么意思
- 中学生作文大全是什么意思
- 中学生作文宝典是什么意思
- 中学生作文手册是什么意思
- 中学生作文指南是什么意思
- 中学生作文描写手册是什么意思
- 中学生作文描写辞典是什么意思
- 中学生作文片断·语汇手册是什么意思
- 中学生作文论据手册是什么意思
- 中学生作文词语分类手册是什么意思