有理数乘法法则

---

两数相乘，同号得正，异号得负，绝对值相乘．任何数与0相乘，积仍为0．

注意 1．几个有理数相乘，因数都不为0时，积的符号由负因数的个数决定．当负因数有奇数个时，积为负；当负因数有偶数个时，积为正．积的绝对值等于各个因数绝对值的积．

2．几个有理数相乘，有一个因数为0时，积为0．

3．在有理数运算中，乘法交换律，乘法结合律、乘法分配律仍然成立．

4．因数中有带分数时，须化成假分数，再相乘．

5．类似－9917/18×9这种题目，注意拆项的技巧．把－9917/18拆成－100+1/18再与9相乘．

例1 计算

(－100)×(－20)－(－3)=＿＿．

答 2003．

[解析] 原式=2000+3=2003．

例2 观察下列各式：

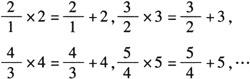
想一想什么样的两数之积等于两数之和?设n表示正整数，用关于n的等式表示这个规律为：＿＿＿＿=＿＿+＿＿．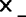

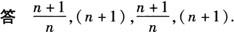
例3 计算

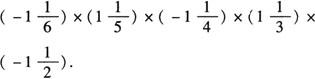
解 原式

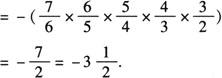
[解析] 几个不等于0的数相乘，积的符号由负因数的个数决定：负因数有奇数个，积为负；负因数有偶数个，积为正，积的符号确定之后，其余运算与小学的求积方法相同．

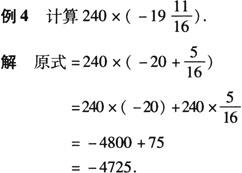
[解析] 合理拆项后利用乘法分配律．