纳入模型

---

如果在任何阶段，一个模型都是另一个更一般模型的特殊情形，就说第一个模型是后一个的纳入模型。

用M_i表示建于数据过程之上的模型，如果模型M₁的参数空间B₁是模型M₂的参数空间B₂的子空间：B₁≤B₂，则称模型是模型的纳入模型，记作M₁≤M₂举例说明，用{x_t}表示由n个随机变量构成的随机过程向量，用

X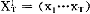=(x₁…x_T)

表示随机过程由时端点1至T的样本，初始条件记作

X₀=(…x_－r…x_－1x₀)

相对于t的过去样本记作

X_t－1=(X₀∶X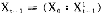_－1)

其中

X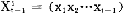_－1=(x₁x₂…x_t－1)

我们将{X_t}的数据生成过程记成：

D_x(X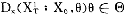∶X₀，θ)θ∈

其中的参数向量θ为k维向量，参数空间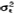是k维子空间。

设残差ε_t服从均值为零，方差为σ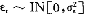的独立正态分布，即ε_t～IN[0，σ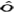]，y_t为t时期的观测值，α为常数，则过程

y_t=y_t－1+α+ε_t

是上述数据生成过程的纳入模型。