两个平面平行的判定定理
两个平面平行的判定定理liangge pingmian pingxing depanding dingli
若一个平面内有两条相交直线都平行于另一个平面,则这两个平面平行.
如图1,若a,b为平面β内的两条相交直线,a∥a,b∥a,则a∥β.

图1
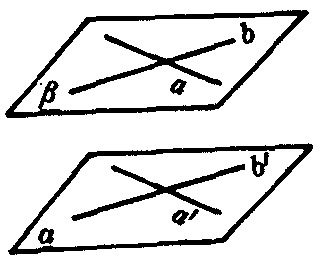
图2
由上述定理可推得:若一个平面内的两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行.
如图2,若a,b为平面β内的两条相交直线,a′,b′为平面a内的两条直线,且a∥a′,b∥b′,则α∥β.
另外,还有一个常用的判定定理:垂直于同一条直线的两个平面平行.
如图3,若l⊥α,l⊥β,则α∥β.

图3
例 已知a,b是两条异面直线.求证经过a而平行于b的平面,必和经过b而平行a的平面平行.
证法1 如图4,在a上任取一点M,过M和b作平面γ,则γ与a相交,设交线为c.因为b∥a,所以b∥c.因此c∥β,又因为α∥β,且a∩c=M,所以α∥β.
证法2 如图5,设AA′为a,b的公垂线,过AA′和b作平面γ与a交于c.因为b∥a,所以b∥c.因为AA′⊥b,所以AA′⊥c.又AA′⊥a,a∩c=A,所以AA′⊥α.同理可证AA′⊥β,于是α∥β.

图4

图5
☚ 两个平面相交 两个平面平行的性质定理 ☛
- 宝坻县织带厂是什么意思
- 宝坻县经济开发区是什么意思
- 宝坻县结核病防治所是什么意思
- 宝坻县职工卫生学校是什么意思
- 宝坻县袁罗庄乡是什么意思
- 宝坻县贫下中农协会是什么意思
- 宝坻县赵各庄乡是什么意思
- 宝坻县还乡团是什么意思
- 宝坻县郝各庄乡是什么意思
- 宝坻县酿酒厂是什么意思
- 宝坻县防疫站是什么意思
- 宝坻县霍各庄乡是什么意思
- 宝坻县饮食服务公司是什么意思
- 宝坻县马家店乡是什么意思
- 宝坻县驻防是什么意思
- 宝坻县高家庄乡是什么意思
- 宝坻县黄庄乡是什么意思
- 宝坻县黄庄第一职专是什么意思
- 宝坻县黑狼口乡是什么意思
- 宝坻图书馆是什么意思
- 宝坻城关医院是什么意思
- 宝坻大张各庄古墓是什么意思
- 宝坻大觉寺是什么意思
- 宝坻宾馆是什么意思
- 宝坻师范附属小学是什么意思
- 宝坻影剧院是什么意思
- 宝坻教师进修学校是什么意思
- 宝坻教育委员会是什么意思
- 宝坻文化广场是什么意思
- 宝坻新华书店是什么意思
- 宝坻旧县志是什么意思
- 宝坻朝阳饭店是什么意思
- 宝坻电影公司是什么意思
- 宝坻盐使司是什么意思
- 宝坻石经幢是什么意思
- 宝坻站是什么意思
- 宝坻红皮大蒜是什么意思
- 宝坻耀阳纺织有限公司是什么意思
- 宝坻育英中学是什么意思
- 宝坻自卫团是什么意思
- 宝坻西李各庄辽墓是什么意思
- 宝坻进出口商品检验局是什么意思
- 宝坻镜是什么意思
- 宝坻饭店是什么意思
- 宝城是什么意思
- 宝城宝顶是什么意思
- 宝埒是什么意思
- 宝堂寺是什么意思
- 宝塔是什么意思
- 宝塔千帆外,春城万壑中。是什么意思
- 宝塔寺塔是什么意思
- 宝塔小学学潮是什么意思
- 宝塔尖上的警报是什么意思
- 宝塔山是什么意思
- 宝塔山宝塔是什么意思
- 宝塔工资是什么意思
- 宝塔式繁育体系是什么意思
- 宝塔石是什么意思
- 宝塔税是什么意思
- 宝塔筒子是什么意思