粘滞性流体的分析方法

---

粘滞性流体在流速不过大时是分层流动的，各层间的流速不同，存在速度分布。

实验指出，若流体层平行于XZ平面且沿X轴方向流动，则相邻层之间单位面积的内摩擦力F／S与速度梯度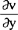成比例即

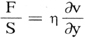
式中η称为流体的粘滞系数。据此可推知半径为R的园管中的粘滞流体的流量为

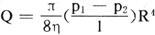
此式称为泊肃叶公式，式中p₁－p₂是管长为L的两端的压强差。还可推知，在粘滞流体中以高速V运动的半径为R的小球所受到的粘滞力为

F=6πηVR

式称为斯托克斯公式。在粘滞流体中自由下落小球最后必达到恒速V_s，此时有

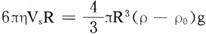
式中ρ及ρ₀分别是小球与流体的质量密度。

于是得

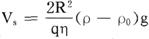
由公式及泊肃叶公式都可用来测定粘滞流体的粘滞系数。

对于如右图所示的粘滞流体，伯努利方程应推广为

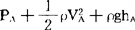表示单位重量的流体由A流到B的过程中由粘滞性导致的阻力所作的功的绝对值。

实验发现，粘滞性流体中，流速超过某一临乔值Vc的地方会产生湍流，即该处附近的流体不再分层流动，变得紊乱，且可出现许多涡旋。实验上还发现，在直径为d的管中流动的质量密度为ρ的粘滞流体的临界流速为

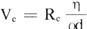
式中R_c称为临界雷诺数。

有时也常引入实际雷诺数

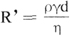
以作为判断管中流动的是层流还是湍流的判据。普通自来水管R_c约在1200到2000的范围内。